Non-linear Models

Not all separable problems are linearly separable. A straight line in not the best decision boundary in many cases.

Let's look at a separable problem that can't be linearly separated:

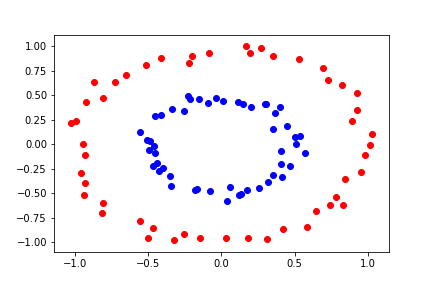
If we try to use a linear model and logistic regression we do not get a good result.

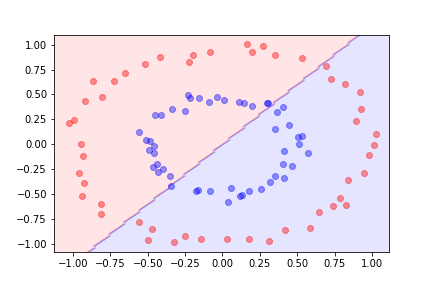
Transforming the features

In order to be able to separate the two sets linearly. We need to process the data before it is possible. If instead of trying to separate the datasets using $x$ and $y$ we can use transformed features. Let's use $x^2$ and $y^2$.

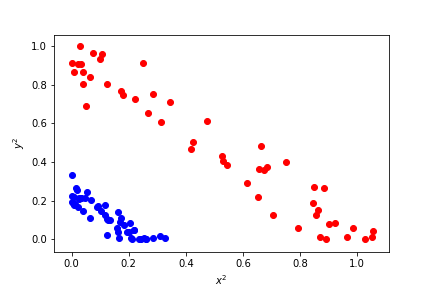
Now we can separate the data linearly!

Adding polynomial features

In general it is difficult to guess which transformation will help separating the data.

By adding polynomial features constructed from the existing ones such as

$$ (x, y) \rightarrow (x, y, x^2, y^2, xy)$$

we increase our separating power. Effectively we allow the straight lines in the linear model to become arbitrary curves if enough polynomial orders are added.

Using quadratic features in addition to the original ones we can separate the datasets using logistic regression on the augmented feature space.

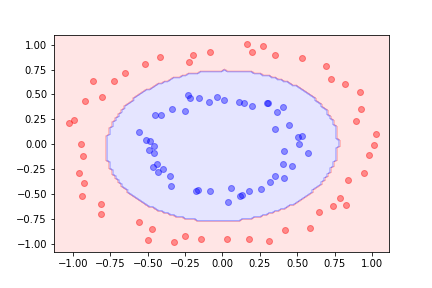
For more complicated boundaries we can include more polynomial features.

Higher order polynomial coefficients

Let's look at a different dataset:

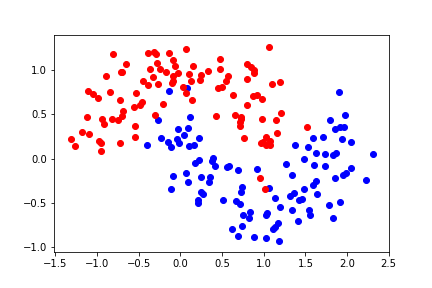
It is not linearly separable. Let's try second order polynomial features.

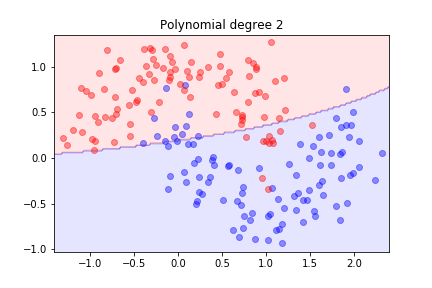
Second order is not sufficient, let's try three...

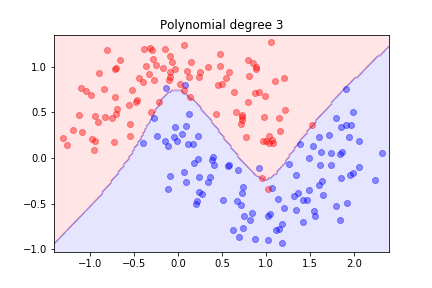
Better! What happens with higher orders?

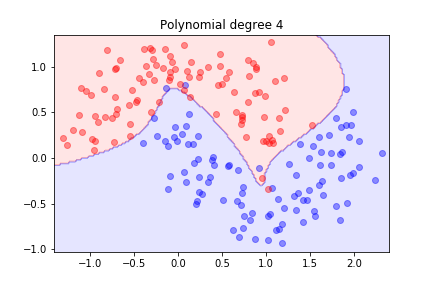
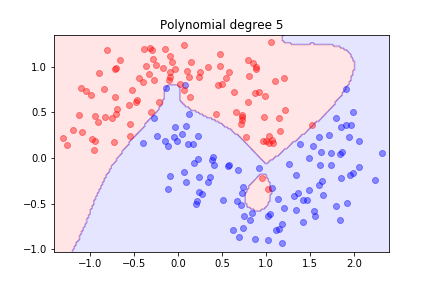
The model is trying hard to separate the data, but it might not generalise well.